Python Data Structures and Algorithms Full Course

Python Data Structures and Algorithms Full Course: Beginner to Advanced 2026

Welcome to this comprehensive guide on Python Data Structures and Algorithms. Whether you're just starting out with programming or looking to deepen your knowledge, this course covers everything from the basics to more advanced topics. In today's fast-paced tech world, understanding Python Data Structures and Algorithms is essential for building efficient applications, solving complex problems, and excelling in coding interviews. Python's simplicity makes it an ideal language for learning these concepts, and by the end of this post, you'll have a solid foundation to apply them in real-world scenarios.

Python Data Structures and Algorithms form the backbone of efficient coding. Data structures help organize and store data effectively, while algorithms provide step-by-step procedures to manipulate that data. Together, they enable developers to optimize performance, reduce resource usage, and create scalable software. This guide is updated for 2026, incorporating the latest best practices in Python 3.12 and beyond. We'll explore built-in structures first, then move to custom implementations, and finally dive into key algorithms with practical examples.

Why focus on Python Data Structures and Algorithms? Python's extensive libraries and readable syntax make it easier to grasp these ideas compared to lower-level languages. Plus, with the rise of AI, machine learning, and data science, mastering these topics opens doors to high-demand careers. Let's begin with the fundamentals.

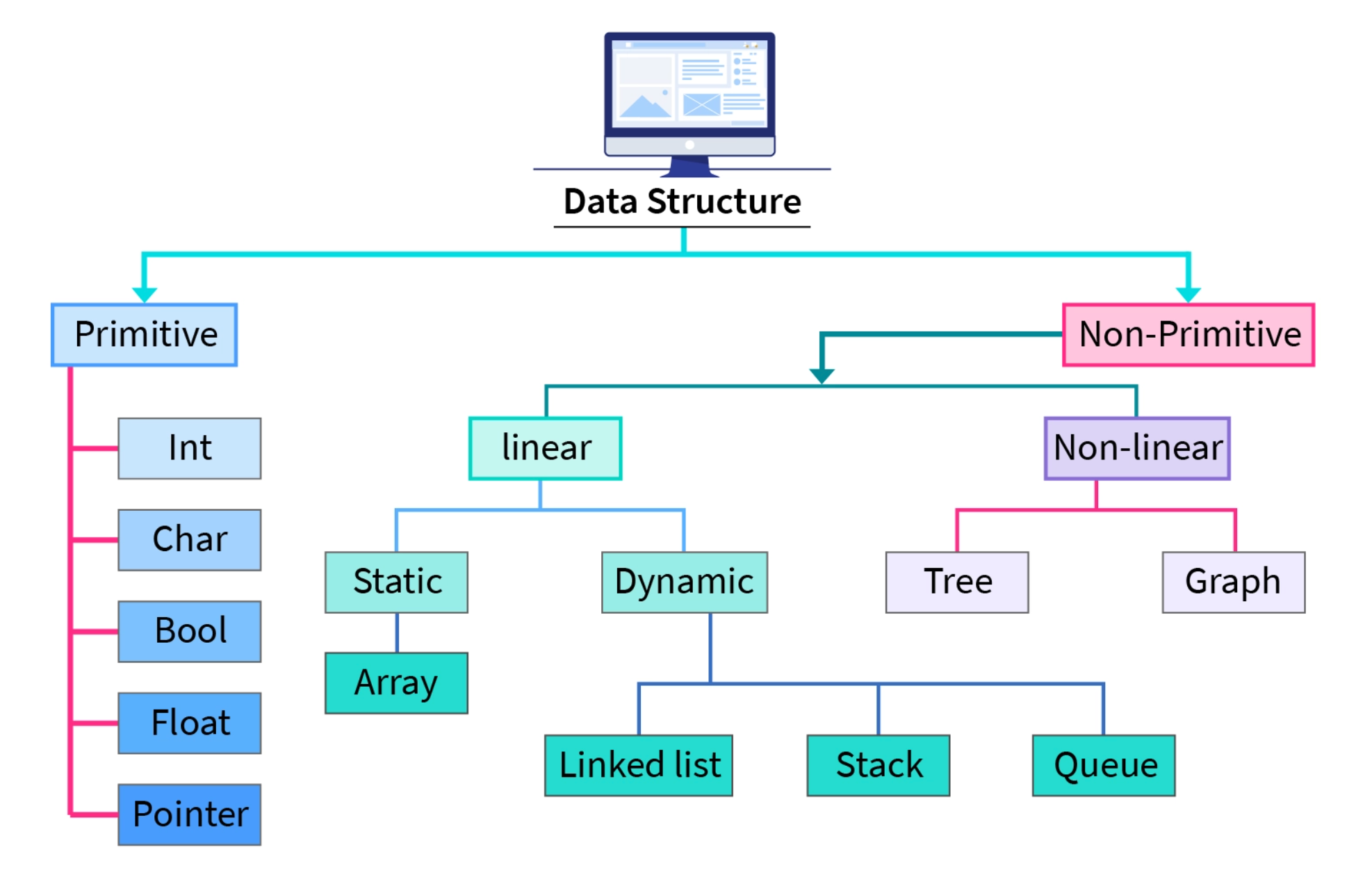
Understanding Data Structures in Python

Data structures are ways to store and organize data so that it can be accessed and modified efficiently. In Python, some are built-in, while others require implementation. Mastering Python Data Structures and Algorithms starts with knowing when to use each type.

Python Lists: Versatile and Dynamic

Lists are one of the most commonly used data structures in Python. They are ordered collections that can hold items of different types, and they are mutable, meaning you can change their contents after creation.

To create a list, use square brackets:

my_list = [1, 2, 3, 'hello', True]

You can access elements by index, starting from 0:

print(my_list[0])  # Output: 1

Lists support slicing, which lets you extract subsets:

subset = my_list[1:3]  # [2, 3]

Adding elements is straightforward with append():

my_list.append(4)

Or insert at a specific position:

my_list.insert(1, 'new')

Removing items can be done with remove() or pop():

my_list.remove('hello')
popped = my_list.pop()  # Removes and returns the last item

Lists are ideal for scenarios where order matters and frequent modifications are needed, like managing a to-do list app.

Performance-wise, accessing elements is O(1), but inserting or deleting at the beginning is O(n) because it shifts elements. For large datasets, consider alternatives if efficiency is critical.

Lists can be nested for multi-dimensional structures:

matrix = [[1, 2], [3, 4]]

Iterating over lists is easy with loops:

for item in my_list:
    print(item)

Or using list comprehensions for concise operations:

squared = [x**2 for x in range(5)]  # [0, 1, 4, 9, 16]

In Python Data Structures and Algorithms, lists are foundational because many algorithms, like sorting, operate on them directly.

Here's a visual representation of how a Python list might look internally:

python.plainenglish.io

Understanding Python Data Structures: From Basics to Advanced | by ...

Python Tuples: Immutable Sequences

Tuples are similar to lists but immutable, meaning once created, their elements can't be changed. This makes them suitable for fixed data, like coordinates or constants.

Create a tuple with parentheses:

my_tuple = (1, 2, 3, 'world')

Access is like lists:

print(my_tuple[1])  # 2

Tuples support slicing too:

sub_tuple = my_tuple[0:2]  # (1, 2)

Since they're immutable, attempts to modify raise errors:

# my_tuple[0] = 4  # TypeError

Tuples are faster than lists for iteration and use less memory, making them great for read-only data in Python Data Structures and Algorithms.

They can be used as dictionary keys because they're hashable:

coord_dict = {(0,0): 'origin'}

Unpacking tuples is handy:

a, b, c, d = my_tuple

In functions, tuples allow returning multiple values:

def get_min_max(numbers):
    return min(numbers), max(numbers)

Tuples shine in scenarios requiring data integrity, like database records.

For a diagram illustrating a Python tuple:

almabetter.com

Tuples and Sets in Python

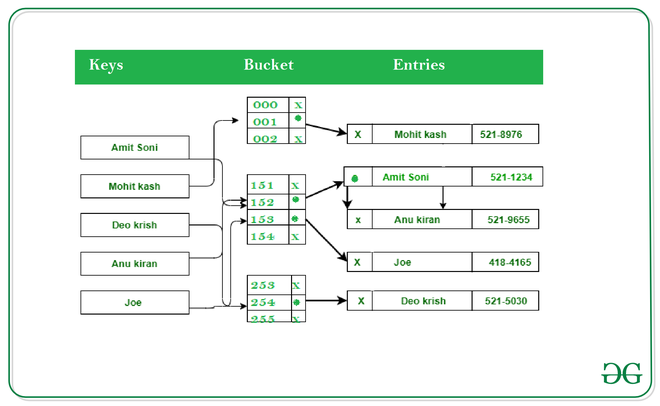
Python Dictionaries: Key-Value Pairs for Fast Lookups

Dictionaries store data in key-value pairs, allowing quick access via keys. They're unordered (before Python 3.7) but insertion-ordered now.

Create one with curly braces:

my_dict = {'name': 'Alice', 'age': 30, 'city': 'New York'}

Access values:

print(my_dict['name'])  # Alice

Add or update:

my_dict['job'] = 'Engineer'

Remove with del or pop():

del my_dict['age']
job = my_dict.pop('job')

Iterate over keys, values, or items:

for key in my_dict:
    print(key)
    
for value in my_dict.values():
    print(value)
    
for key, value in my_dict.items():
    print(f"{key}: {value}")

Dictionaries use hashing for O(1) average-case lookups, making them essential in Python Data Structures and Algorithms for caching or mapping.

Nested dictionaries handle complex data:

users = {'user1': {'name': 'Bob', 'age': 25}}

Dictionary comprehensions:

squares = {x: x**2 for x in range(5)}

In real-world apps, dictionaries power JSON handling and API responses.

See this internal structure of a Python dictionary:

geeksforgeeks.org

Internal Structure of Python Dictionary - GeeksforGeeks

Python Sets: Unique Elements for Membership Testing

Sets are unordered collections of unique items, perfect for eliminating duplicates and fast membership checks.

Create with curly braces or set():

my_set = {1, 2, 3, 2}  # {1, 2, 3}

Add elements:

my_set.add(4)

Remove:

my_set.remove(2)  # Raises KeyError if not found
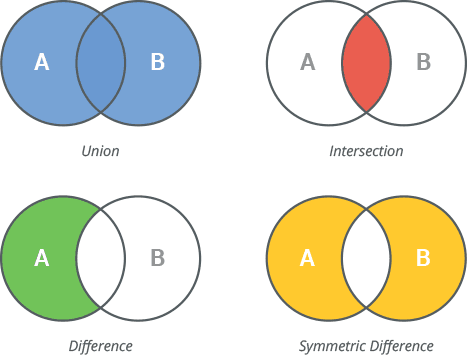
my_set.discard(5)  # No error if not found

Set operations like union, intersection:

set1 = {1, 2, 3}
set2 = {3, 4, 5}
union = set1 | set2  # {1,2,3,4,5}
intersection = set1 & set2  # {3}
difference = set1 - set2  # {1,2}

Sets are hash-based, offering O(1) lookups, additions, and deletions on average.

In Python Data Structures and Algorithms, sets are used in graph problems for visited nodes or unique paths.

Frozen sets are immutable versions:

frozen = frozenset([1,2,3])

Iterate easily:

for item in my_set:
    print(item)

Sets help in data cleaning, like removing duplicates from lists:

unique = set([1,1,2,3,3])

Here's a diagram of Python set operations:

learnbyexample.org

Python Set - Learn By Example

Implementing Advanced Data Structures in Python

While Python provides built-ins, understanding custom data structures is key to mastering Python Data Structures and Algorithms.

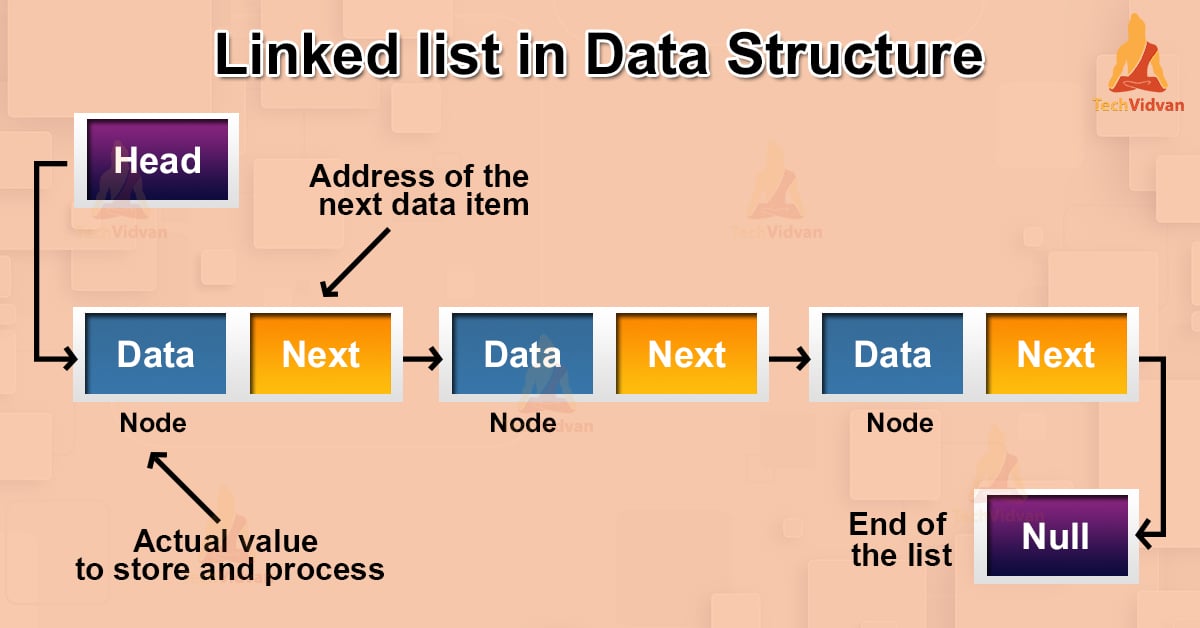
Linked Lists: Flexible Node-Based Structures

Linked lists consist of nodes, each containing data and a reference to the next node.

Implement a simple singly linked list:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None
    
    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            return
        last = self.head
        while last.next:
            last = last.next
        last.next = new_node
    
    def print_list(self):
        current = self.head
        while current:
            print(current.data, end=' -> ')
            current = current.next
        print('None')

Usage:

ll = LinkedList()
ll.append(1)
ll.append(2)
ll.print_list()  # 1 -> 2 -> None

Insertion at beginning is O(1), but searching is O(n). Linked lists are useful for frequent insertions/deletions without shifting.

Doubly linked lists add previous pointers for bidirectional traversal.

In Python Data Structures and Algorithms, linked lists form the basis for stacks and queues.

Visualize a linked list:

techvidvan.com

Linked List in Data Structure - TechVidvan

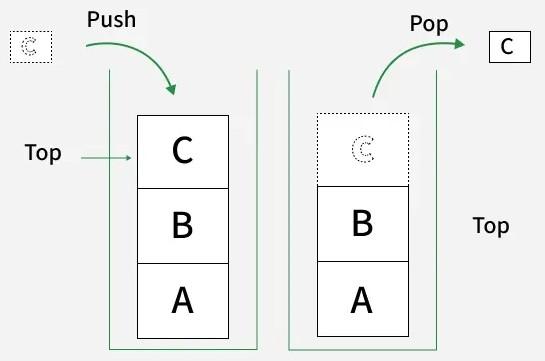
Stacks: Last-In, First-Out (LIFO)

Stacks follow LIFO principle, like a stack of plates.

Use lists for simple stacks:

stack = []
stack.append(1)  # Push
stack.append(2)
print(stack.pop())  # 2 (Pop)

For thread-safety, use collections.deque:

from collections import deque
stack = deque()
stack.append(1)
stack.append(2)
print(stack.pop())  # 2

Stacks are used in function calls, undo mechanisms, and parsing expressions.

Implement with linked list for practice.

In algorithms, stacks help in depth-first search and backtracking.

Illustration of a stack:

geeksforgeeks.org

Introduction to Stack Data Structure - GeeksforGeeks

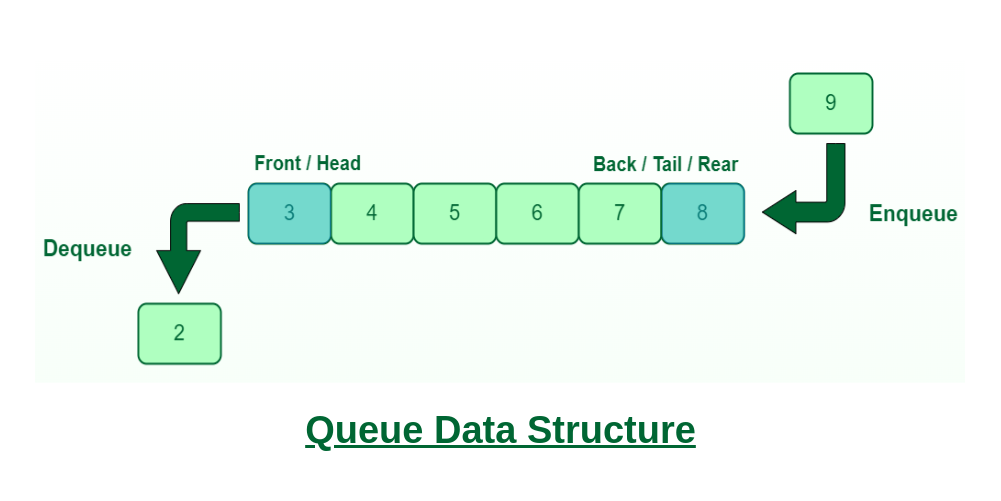
Queues: First-In, First-Out (FIFO)

Queues are FIFO, like a line at a store.

Use deque for efficiency:

from collections import deque
queue = deque()
queue.append(1)  # Enqueue
queue.append(2)
print(queue.popleft())  # 1 (Dequeue)

Lists are inefficient for queues due to O(n) shifts.

Queues are crucial in breadth-first search, task scheduling, and buffering.

Priority queues use heapq:

import heapq
pq = []
heapq.heappush(pq, (2, 'task2'))
heapq.heappush(pq, (1, 'task1'))
print(heapq.heappop(pq))  # (1, 'task1')

In Python Data Structures and Algorithms, queues manage order in simulations.

Diagram of a queue:

geeksforgeeks.org

What is Queue Data Structure? - GeeksforGeeks

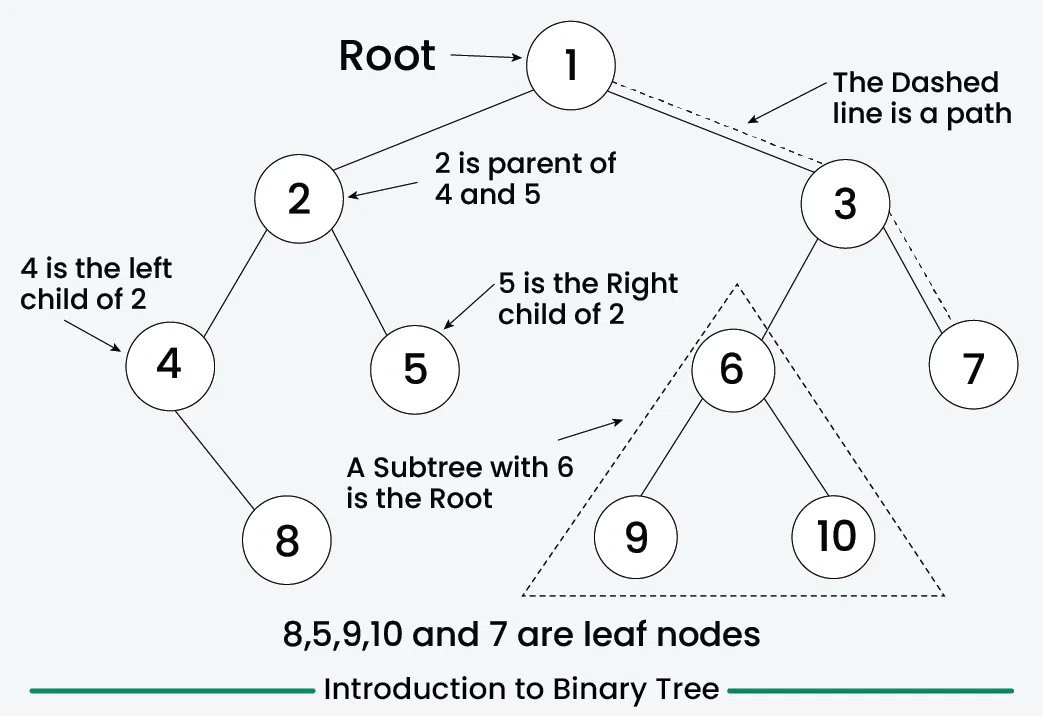
Trees: Hierarchical Structures

Trees have nodes with children, rooted at the top.

Binary trees limit two children per node.

Implement a binary tree node:

class TreeNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

Traversal methods: inorder, preorder, postorder.

Inorder:

def inorder(node):
    if node:
        inorder(node.left)
        print(node.data)
        inorder(node.right)

Trees are used in file systems, databases (BST for sorted data), and decision trees in ML.

Binary Search Trees (BST) maintain order: left < root < right.

Insertion in BST:

def insert(root, data):
    if not root:
        return TreeNode(data)
    if data < root.data:
        root.left = insert(root.left, data)
    elif data > root.data:
        root.right = insert(root.right, data)
    return root

In Python Data Structures and Algorithms, trees enable efficient searching O(log n).

View a binary tree:

geeksforgeeks.org

Binary Tree Data Structure - GeeksforGeeks

Graphs: Networks of Nodes and Edges

Graphs consist of vertices and edges, directed or undirected.

Represent as adjacency list:

graph = {
    'A': ['B', 'C'],
    'B': ['D'],
    'C': ['D'],
    'D': []
}

Or using defaultdict:

from collections import defaultdict
graph = defaultdict(list)
graph['A'].append('B')

Graphs model social networks, maps, and web pages.

Traversal: DFS (stack), BFS (queue).

BFS example:

from collections import deque
def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node)
            visited.add(node)
            queue.extend(graph[node])

In Python Data Structures and Algorithms, graphs are central to shortest path problems.

Diagram of a graph:

upgrad.com

Types of Graphs in Data Structures You Probably Missed!

Fundamentals of Algorithms in Python

Algorithms are sets of instructions to solve problems. In Python Data Structures and Algorithms, efficiency is measured by time and space complexity using Big O notation.

O(1) is constant time, O(n) linear, O(log n) logarithmic, O(n^2) quadratic.

Always analyze algorithms for worst-case scenarios.

Python's sorted() is O(n log n), but understanding implementations builds skills.

Searching Algorithms

Searching finds elements in data structures.

Linear Search

Scans sequentially:

def linear_search(arr, target):
    for i, val in enumerate(arr):
        if val == target:
            return i
    return -1

O(n) time, simple for unsorted data.

Binary Search

For sorted arrays, halves the search space:

def binary_search(arr, target):
    low, high = 0, len(arr) - 1
    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1
    return -1

O(log n) time, efficient for large sorted lists.

In Python Data Structures and Algorithms, binary search is a staple for optimization.

Here's a diagram of binary search:

youtube.com

Binary Search Algorithm (Working, Algorithm & Diagram) in Data Structures | Part 1 | DSA

Sorting Algorithms

Sorting arranges elements in order.

Bubble Sort

Compares adjacent elements, swaps if out of order:

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

O(n^2) time, simple but inefficient for large n.

Insertion Sort

Builds sorted list by inserting elements:

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key
    return arr

O(n^2), good for small or nearly sorted data.

Selection Sort

Selects minimum and swaps:

def selection_sort(arr):
    for i in range(len(arr)):
        min_idx = i
        for j in range(i+1, len(arr)):
            if arr[min_idx] > arr[j]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

O(n^2), not adaptive.

Merge Sort

Divide and conquer, merges sorted halves:

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        left = merge_sort(arr[:mid])
        right = merge_sort(arr[mid:])
        
        i = j = k = 0
        while i < len(left) and j < len(right):
            if left[i] < right[j]:
                arr[k] = left[i]
                i += 1
            else:
                arr[k] = right[j]
                j += 1
            k += 1
        
        while i < len(left):
            arr[k] = left[i]
            i += 1
            k += 1
        while j < len(right):
            arr[k] = right[j]
            j += 1
            k += 1
    return arr

O(n log n), stable and efficient.

Steps of merge sort:

youtube.com

Merge sort algorithm

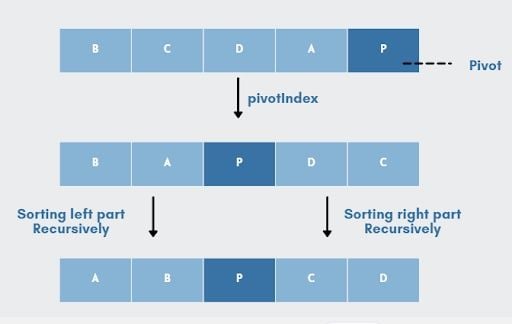
Quick Sort

Pivots and partitions:

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr)//2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

Average O(n log n), worst O(n^2), but fast in practice.

Pivot in quick sort:

builtin.com

Quicksort Algorithm: An Overview | Built In

In Python Data Structures and Algorithms, choose sorting based on data size and characteristics.

Visualization of bubble sort:

youtube.com

Bubble Sort

Graph Algorithms

Breadth-First Search (BFS)

Level-order traversal, uses queue.

As shown earlier.

Shortest path in unweighted graphs.

Depth-First Search (DFS)

Explores deep, uses stack or recursion:

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

Detects cycles, topological sort.

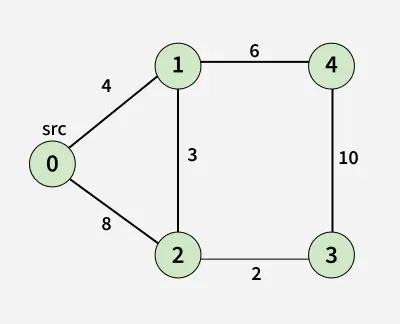
Dijkstra's Algorithm

Shortest path in weighted graphs:

import heapq
def dijkstra(graph, start):
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    pq = [(0, start)]
    while pq:
        dist, node = heapq.heappop(pq)
        if dist > distances[node]:
            continue
        for neighbor, weight in graph[node]:
            new_dist = dist + weight
            if new_dist < distances[neighbor]:
                distances[neighbor] = new_dist
                heapq.heappush(pq, (new_dist, neighbor))
    return distances

Assume graph as dict of lists: {'A': [('B', 1), ('C', 4)]}

O((V+E) log V) with heap.

In Python Data Structures and Algorithms, Dijkstra is key for navigation apps.

Graph for Dijkstra:

geeksforgeeks.org

Dijkstra's Algorithm - GeeksforGeeks

Dynamic Programming

DP solves complex problems by breaking into subproblems, storing results to avoid recomputation.

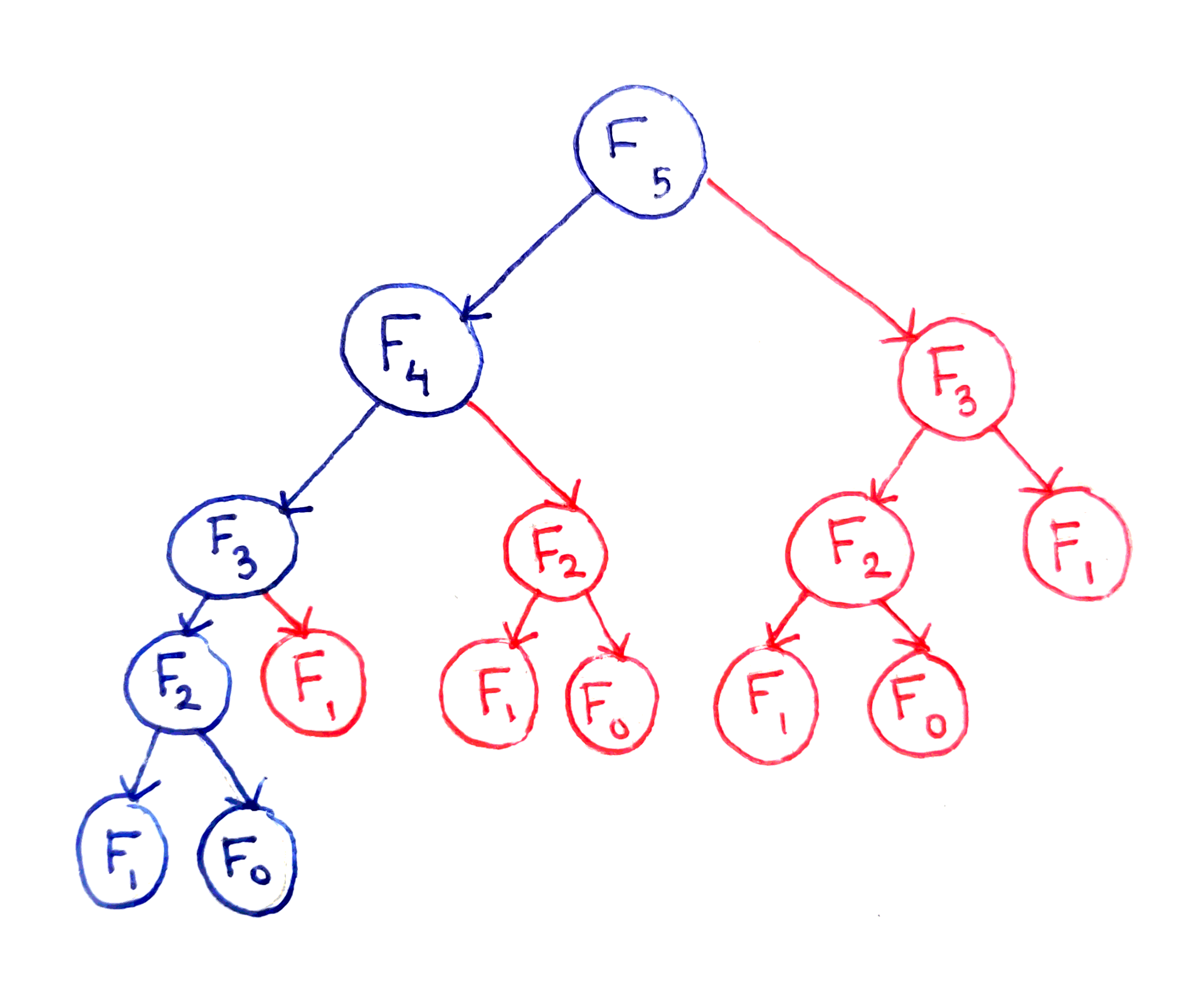
Fibonacci Sequence

Naive recursion is exponential, DP makes it linear.

Memoization:

memo = {}
def fib(n):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fib(n-1) + fib(n-2)
    return memo[n]

Tabulation:

def fib_tab(n):
    if n <= 1:
        return n
    table = [0] * (n+1)
    table[1] = 1
    for i in range(2, n+1):
        table[i] = table[i-1] + table[i-2]
    return table[n]

O(n) time and space.

0/1 Knapsack

Maximize value without exceeding weight:

def knapsack(weights, values, capacity):
    n = len(values)
    dp = [[0 for _ in range(capacity+1)] for _ in range(n+1)]
    for i in range(1, n+1):
        for w in range(1, capacity+1):
            if weights[i-1] <= w:
                dp[i][w] = max(values[i-1] + dp[i-1][w - weights[i-1]], dp[i-1][w])
            else:
                dp[i][w] = dp[i-1][w]
    return dp[n][capacity]

O(n*capacity) time.

DP is powerful in optimization problems within Python Data Structures and Algorithms.

Fibonacci tree in DP:

avikdas.com

A graphical introduction to dynamic programming

Conclusion

This full course on Python Data Structures and Algorithms has taken you from beginner concepts like lists and tuples to advanced topics like dynamic programming and graph algorithms. Practice these with real projects to solidify your understanding. In 2026, with Python evolving, these skills remain timeless for efficient coding. Keep exploring, and you'll master Python Data Structures and Algorithms for any challenge.